Bezug → Rechenbeispiel Pizza
.................................................
Die Kreiszahl π hat (näherungsweise) den Wert 3,14;
Die Fläche eines Kreises wird so berechnet:
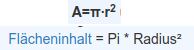
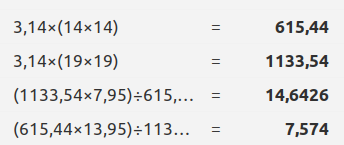
Wir benutzen den 'Dreisatz' zur Berechnung dessen, was eine große Pizza kosten würde, wenn man den Preis der kleinen zugrunde legt - und umgekehrt.
615,44 ≙ 7,95
1133,54 ≙ x
x = 14,64 [€]
und
1133,54 ≙ 13,95
615,44 ≙ x
x = 7,57 [€]
Das Ergebnis zeigt: Die große Pizza ist pro Flächeneinheit die preiswertere Lösung
Aber:
Noch interessanter wäre die Frage ob es günstiger ist 2x die kleine Pizza zu nehmen oder 1x die große?
Was meinen Sie?
Wie beweisen Sie das?

Sie erinnern mich an Zeiten, als ich beim Aldi stand und ausrechnete, welches denn nun wirklich die allerbilligsten (Autokorrektur schreibt "Allerheiligsten") Erbsen im Glas sind, denn nur die erlaubte mir mein kostenbewusstes Gewissen zu kaufen.
Schauen Sie in Ihren Geldbeutel - sind noch 15,90 Euro drin, bestellen Sie zweimal eine kleine Pizza. Sind nur noch 13,95 Euro drin, nehmen Sie eine große und schneiden sie durch. (Nicht vergessen: Trinkgeld für den Lieferservice mit einkalkulieren!)
Guten Appetit!
Ach wie gut, dass es noch Menschen gibt die pragmatische Lösungen vorschlagen ohne lange & kompliziertere Wege zu verfolgen.
Da es sich nicht um ein aktuelles Problem handelt, sonder um ein seit Jahren zurückliegendes Ereignis in einem fremden Blog (zu dem ich verlinkt hatte) und das nicht mehr 'aktiv' ist, wollte ich einen Ansatz aufzeigen wie ich es damals 'gelöst' habe.
Pizza ist - so pflege ich zu schreiben - kein Essen sondern allenfalls ein Snack, weswegen es auf unserem Speisezettel nur dann vorkommt wenn wir und entscheiden "junkfood"-Tag" einzulegen und McDonalds und BurgerKing sind beie zu ....