"Selbstzweckformel", sondern ....
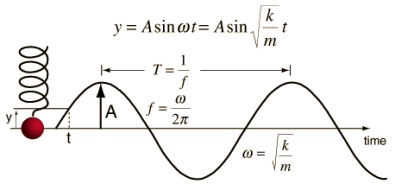
die Berechnung der Schwingung einer Feder, hier mit einem Gewicht, dessen Ausgangslage auf der Zeitlinie "time" (= x-Achse) dargestellt ist. Man spricht auch von einer "Oszillationskurve".

Wie aus der Abbildung zu sehen ist, kann man die Rotation auf einem Kreis entlang der x-Achse projezieren und erhält so eine Sinus-Kurve. Diese ist abhängig von der Geschwindigkeit, mit der "P" um den Mittelpunkt rotiert.
Der Abstand zwischen "N" und "P" entspricht "t" in der oberen Zeichnung.
Die Frequenz (=Rotationsgeschwindigkeit) f=ω/2π bestimmt den Abstand der Umkehrpunkte der Sinuskurve, bezeichnet mit "T", einem absoluten Zeitintervall, deswegen ist f=1/T=ω/2π; während dieses Intervalls schwingt die Kugel (an der Feder) vom höchsten Auslenkungspunkt zum tiefsten Punkt und wieder zurück, in der Kreisabbildung rotiert P einmal um den Kreis.
Die Amplitude "A" stellt den Abstand von der Null-Linie dar und geht von +A bis -A, sie ist der jeweils maximale Abstand auf der y-Achse (in der Abbildung mit dem Kreis heißen die Punkte "+1" und "-1").
Mit "t" wird ein bestimmter Zeitpunkt bezeichnet, der kleiner ist als das absolute Zeitintervall "T"; man könnte also die Addition mehrerer "t" ausführen - maximal addieren sich diese zu "T" (weil sonst eine nächste Schwingung beginnen würde).
Ganz einfach gesagt:
Es wird dargestellt, mit welcher Kraft die Feder schwingt ....
und das ist nach dieser Darstellung vom Gewicht der Kugel (rot) abhängig ....
PS
Das "ω" ist kein "w", sondern ein (kleines) "omega"; Das große "Omega" sieht dann so "Ω" aus ....
2 PS
In Wirklichkeit sind solche Schwingungen immer "Gedämpfte Schwingungen", d.h. sie werden immer kleiner, je länger sie andauern. Der Grund dafür ist der Luftwiderstand, der Reibung erzeugt und der Federkraft entgegenwirkt. Daher sieht die Kurve üblicherweise so aus:
[Quelle f. untere Abbildung]