Kürzlich hatte ich darüber geschrieben, dass Wissenschaftler nicht gleich kompetent über jedwedes Fachgebiet Aussagen treffen können. Nun bin ich auf ein Video des bekannten Fernsehprofessors Lesch gestoßen und an einem Satz hängengeblieben - der lautet:
" .. Es lassen sich keine geschlechtsspezifischen Ausprägungen bestimmter [Gehirn-] Areale erkennen. Tatsächlich sind die Unterschiede der Fähigkeiten innerhalb eines Geschlechts größer als zwischen den Geschlechtern .. "
[Ab 04:12 min im Video]
Bei diesen Untersuchungen ging es um Orientierung, mit besonderer Fragestellung ob sich die Leistungen unterscheiden und ob sich Unterschiede sichtbar machen lassen (per CT¹).
Das ist allerdings aus meiner Sicht deswegen unbedeutend, weil der Satz von Prof. Lesch so wie er im Video geäußert wird nicht zutreffend sein kann.
Geht man von einer Variabilität zwischen den Grenzen "hoch" bzw "tief" aus, so muß sich eine Gauß'sche Verteilung ["Normalverteilung"] ergeben, innerhalb derer die Leistungen liegen - und zwar zwei verschiedene Kurven, wenn man Männer und Frauen untersucht. Es ist kaum zu erwarten, dass diese Kurven total identisch sind, alleine durch den Meßfehler müssen Unterschiede vorhanden sein.
Das ergibt zwei Kurvenbilder, die hier nur exemplarisch dargestellt sind und nicht die tatsächlichen Befunde darstellen - allerdings den tatsächlichen Befunden prinzipiell ähnlich sein dürften (Frauen rechts, Männer links):
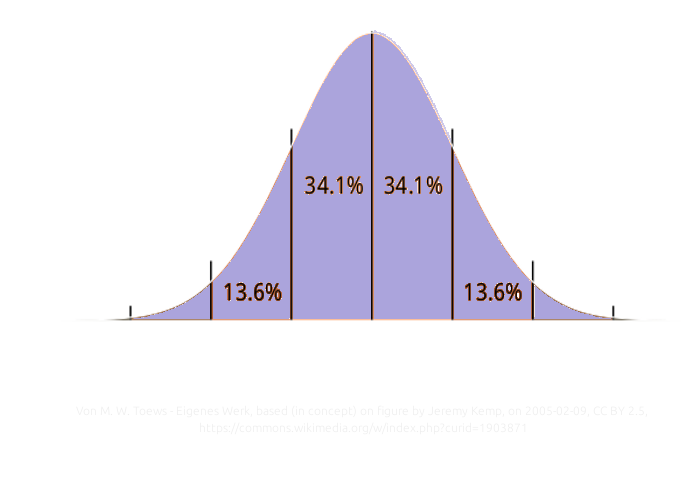
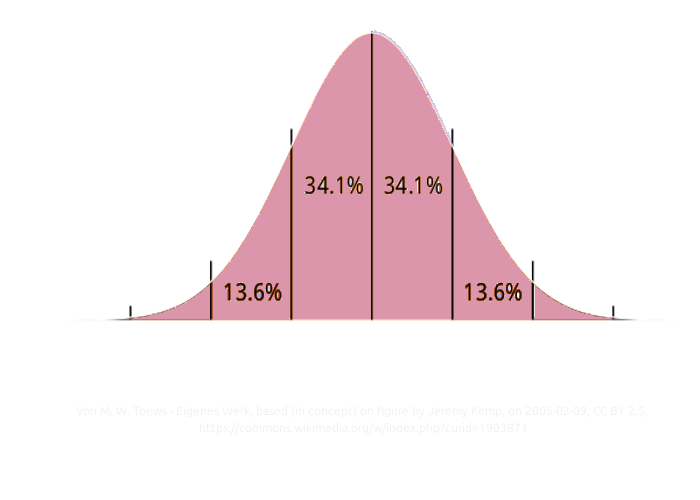
Schiebt man nun diese Kurven übereinander so ergibt sich, dass der Satz von Lesch nicht stimmen kann.
Der Unterschied zwischen den Personen eines Geschlechts kann nicht größer sein als zwischen den Geschlechtern. Die Kurven könnten höchstens nebeneinander liegen - dann wäre der Teil der Aussage " .. größer als zwischen den Geschlechtern .. " falsch.
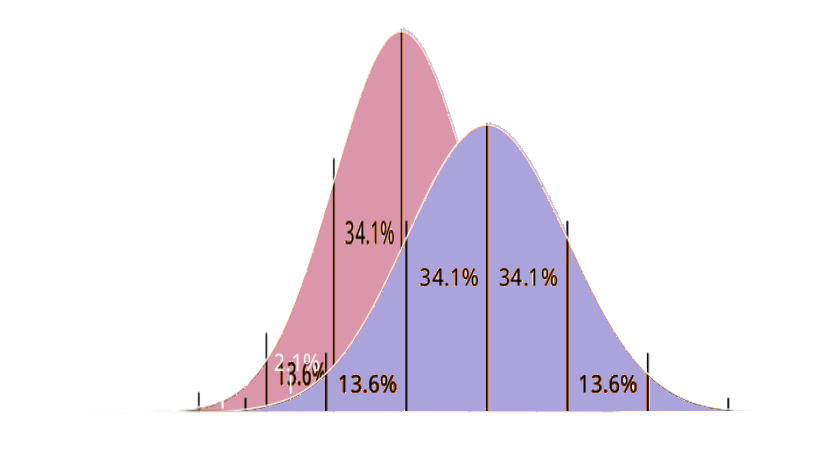
Wenn Befunde 'zwischen den Geschlechtern' größer sein würden, so lägen sie trotzdem kurvenmäßig übereinander - und damit ist die Aussage 'innerhalb eines Geschlechts' nie zutreffend.


Hm... Wenn man es mal aus neuroplastischer Sicht betrachtet, was man aus einem Menschen alles machen kann mit dem richtigen Input, dann dürfte diese Aussage nicht ganz falsch sein.
Das wäre aber ein sehr utopischer Zustand, denn von Außen stehen Menschen um einen herum, die einen auf Grund von ihrer Sicht auf männlich und weiblich in bestimmte Richtungen drängen und/oder fern halten.
Zudem wäre dann noch der Faktor, dass Kind das Geschlecht instinktiv versucht nachzuahmen, wozu es sich selbst zugehörig sieht - und die Leute bieten in der Regel auch ein in bestimmte Richtungen gefärbtes Bild an.
Es wird also nicht passieren, dass ein Kind in der Entwicklung derart vielfältig geprägt wird, sodass sich daraus keine Tendenz eher männlich/eher weiblich assoziierte Interessen bildet und auf Grund dessen Fähigkeiten und Denkweisen bis zum Erwachsenenalter hinein derart gleichmäßig ausgeprägt werden.
Wie gesagt, theoretisch sollte das sogar richtig sein, aber kommt praktisch kaum so vor.
Die Umwelteinflüsse aus dem Milieu des Heranwachsens werden aus meiner (biologisch gefärbten) Sicht stets überschätzt, die sozio-psychologischen sogar noch mehr. Dagegen werden die genetischen Rahmenbedingngen weitestgehend unterschätzt. Einfacher gesagt:Aus einem (genetisch angelegten) Dummkopf wird selbst mit jahrelanger Pädagogik & sonstiger Einflußnahme kein Nobelpreisträger.
Mir ging es hier um zweierlei:
Nicht alles, was von durchaus achteswerten Professoren kommt muss den Tatsachen entsprechen - und zweitens ist es ein weitere Hinweis, dass nicht fachfremd argumentiert werden sollte, weil da oft die Basis fehlt.
Ich weiß ja nicht, aus welchem Hintergrund er heraus seine Aussage formuliert - mit welchem eigenen Erkenntnisstand. Wäre an dieser Stelle wichtig zu wissen.
Deswegen - theoretisch ist die Behauptung nicht ganz falsch, allerdings käme das nur unter utopischen Umständen zustande, welche man selten in der Praxis antrifft.
Das Außen gibt das zu selten her, und dann wären da noch die eigenen inneren Prozesse, die über das willentlich Steuerbare hinausgehen.
Speziell denke ich dabei z. B. an Hormone (pränatale als auch nach der Geburt).
Äußerlich wird man einem Menschen natürlich später nicht ansehen, welcher Hormondusche er im Mutterleib ausgesetzt war - hat ein Mädchen etwas Testosteron abbekommen, kann man sich vielleicht darüber freuen, dass sie Naturwissenschaft interessiert. War das nicht der Fall, muss man sich damit begnügen, dass sie den größten Gefallen an der weiblichen Geschlechtsrolle findet und ihr Wissenschaft einerlei ist.
Das sieht man jemandem weder an, wenn er auf die Welt kommt, noch lässt es sich zielgerichtet steuern oder später noch ändern.
Und Hormone nach der Geburt haben ebenso noch mal ihren ganz eigenen Einfluss...
Wie handhabe ich's so schön? Wenn Testosteron beim Doping nicht funktionieren würde, würde es keiner nehmen.
Also, die bewirken was - körperlich, und dadurch, dass sie damit früher oder später auch auf das Gehirn wirken, ebenso mental. Wobei man sich diese Effekte nicht wie ein Extrem vorstellen darf, sondern mehr wie etwas, was im subtilen Bereich angesiedelt ist.
Für den einen gibt es dabei mehr Probleme mit dem anderen oder dem eigenen Geschlecht (sodass er beginnt, darüber ins Grübeln zu kommen, die Unterschiede in der Tiefe wahrzunehmen), für den anderen weniger (und er nimmt nie etwas wahr).
Die Aussage stammt aus dem verlinkten Video - und dabei geht es um die neuerdings durch fortgeschrittene Technik möglich gewordene Untersuchung von Hirnaktivität bei bestimmten, also definierten Aktivitäten.
Die Rolle der Hormone ist - im Gegensatz zum Nervensystem - langsame Änderungen zu initiieren und im Zusammenspiel mit dem Nervensystem abzusichern. Es geht also um 'große Schwünge', während das nervensystem 'rasche Änderungen' erledigt.
Die Rolle der Hormone bei der Entwicklung ist zwar im Groben umrissen, aber was während verschiedener Stadien der Entwicklung passiert wurde meist aus Tiermodellen erforscht - und deswegen ist eine direkte Analogie nicht immer herzustellen. Mit verfeinerten, weniger belastenden Untersuchungsmethoden wird sich das im Lauf der nächsten Jahre ändern (Nano-Technologie!).
Hm... Kann ja auch sein, dass man durch diese neueren Messverfahren durchaus kleinere Variationen im Durchschnitt findet als das bisher angenommen wurde.
Ein Durchschnitt ist aber nur ein Durchschnitt; da wird "grottenschlecht" mit "sehr gut" zusammengeworfen und beides verschwindet in der großen Masse.
Und aus "besser im Schnitt als man erwartet hätte" wird am Ende doch kein "ist gleich gut".
Wer weiß, warum das da so gesagt wurde... Die Öffentlich-Rechtlichen sind heutzutage auch bei der neueren Political Correctness mit an Bord.
Mein verdacht ist, dass es sich dabei um eine Übersetzung handelt, die irgendwie falsch interpretiert was der ursprüngliche Text aussagen sollte. Oder dass es wegen des Klanges, der Sprachmelodie und der scheinbaren Eleganz so formuliert wurde - wohl wissend, dass es nicht viele Zuhörer geben wird die so pingelig sind wie ich in diesem besonderen Fall ;c)
Das kann natürlich auch sein.
Bei wissenschaftlichen Texten in Fremdsprache muss ich auch oft zwei Mal lesen bzw. das Wörterbuch bemühen, weil sie schwerer zu verstehen sind als alltägliches informelles Gebrabbel.
Bin mal dazu gekommen, das Video anzusehen...
Ist doch besser, man redet über was, was man auch tatsächlich gesehen hat.
Die Grundbotschaft muss ich doch so unterstützen, dass die Unterschiede in den geistigen Fähigkeiten kleiner sind als stets angenommen. Das liegt, für mich, zum einen daran, dass die Gesetze von neuronaler Entwicklung bei beiden doch dieselben sind. Also, es ist eine Frage, welchen Input man jemandem gibt, dementsprechend fallen seine Fähigkeiten aus (zusammen in Kombination mit den Erbanlagen der Eltern).
Siehe die Sache mit der rosa- und blau-farbenen Kleidung. Irgendwo ist mir das einmal schon begegnet, dass das eine Erfindung der Moderne ist. Diese Festlegung, was die adäquate Kleidung für Jungen/Männer und Mädchen/Frauen sind, sah in anderen Jahrhunderten völlig anders aus. Dürfe auch kulturübergreifend seine Unterschiede (gehabt) haben.
Eine andere Sache ist, und darüber habe ich hin und wieder auch schon nachgedacht: War man in der Geschichte tatsächlich so frauenfeindlich wie das immer als selbstverständlich abgetan wird?
An einigen Stellen (die, die ersichtlich sind) erscheint es eher eine Frage der täglichen Arbeitsteilung zu sein als wirkliche Diskriminierung, weil Frauen als minderwertig gesehen wurden. Frauen gab man nicht die schwerste körperliche Arbeit in die Hand, weil man merkte, dass die Männer in dem Bereich leistungsfähiger waren. Umgekehrt, Bereiche, in denen das nicht so ausschlaggebend war - so lang jedenfalls die Religion noch nicht aus dem Nahen Osten nach Europa geschwappt war-, da sah man keinen praktischen Grund, die Frauen auszuschließen. Mehr noch: Wenn man Arbeitskräfte braucht, ist man schön dumm, die eine Hälfte pauschal wegen irgendwelcher Gefühlsduselei auszuschließen.
Die klassische Arbeitsteilung in der Ehe hatte in früheren Jahrhunderten auch noch eine andere Grundlage: Weil der Mann körperlich kräftiger ist, sollte er arbeiten gehen, dafür erledigte sie andere Arbeiten für ihn, um ihm täglich den Rücken frei zu halten, damit er nach der Arbeit das nicht auch noch am Hals hat.
Die Kinder wurden nach Möglichkeit dabei mit eingespannt als Hilfe oder die älteren Geschwister und eventuelle Großeltern haben währenddessen auf die jüngeren Kinder aufgepasst, damit die Mutter sich auf ihren Aufgabenbereich konzentrieren konnte.
Heute benötigt dieser Bereich nicht mehr diese strikten Trennungen, weil es durch allerlei Haushaltsgeräte und Hilfsmittel für das jeweilige Geschlecht physisch möglich ist, auch allein klarzukommen - lediglich kann es sein, dass man eine zweite Person braucht, weil Arbeitsteilung Zeit spart im Gegensatz dazu, wenn jeder im Haushalt alles allein machen muss.
Also kann es dazu kommen, dass in den verschiedenen Individuen ganz andere Fähigkeiten, konträr zur sozialen geschlechtlichen Erwartung, als früher bestärkt und entwickelt werden können. Diese Möglichkeiten waren in früheren Zeiten nicht in dem Maße vorhanden, jedenfalls nicht als Mainstream, eher als Ausnahme (siehe dass in den Adelsgeschlechtern Söhne wie Töchter gleichermaßen gebildet wurden; diese konnten aber auch in wesentlich behüteteren Verhältnissen mit mehr Freiheiten von schwerer Arbeit aufwachsen).
Das würde dann auch erklären, warum es weniger Frauen in der Historie gibt, die für herausragende Leistungen bekannt wurden. Schlichtweg waren sie traditionell nicht in den Positionen, nicht in dem "Job", der eine hohe Wahrscheinlichkeit auf so etwas besaß.
Mit den Zeiten besser werdender Versorgung wurde das möglich. (Mal ebenbei bemerkt: Sind denn auch von Männern von niedrigem Stand in den früheren Jahrhunderten bahnbrechende intellektuelle Leistungen ausgegangen, die man heute noch kennt? Vieles, was in die Geschichte einging, stammt auch entweder von Gelehrten (von Leuten, die durch Institutionen der Kirche Zugang zu Bildung erhielten) oder von solchen, die in einem etwas besser gestellten Elternhaus aufgewachsen sind und so Bildung erhielten. Es sind also auch viele Männer gestorben, ohne jemals ihren Fußabdruck in der menschlichen Geschichte zu hinterlassen.)
Bis jetzt bleibt also der große Durchbruch von Seiten der Frauen eher deshalb auf der Strecke, weil aus diesen Möglichkeiten nicht viel gemacht wird. Traditionelle Rollen und Denkmuster durch dumme Erziehung und durch kapitalistisches Marketing aufrecht erhalten werden, bzw. Manipulation zu neuen unter diesem Dachverband angestiftet wird.
Auch herrscht unter Frauen selbst eine gewisse Mutlosigkeit, ein Mangel zu einem gewissen bisschen Risiko - an Ehrgeiz mangelt den Leistungsbereiten nicht, aber eben daran, ganz selbstverständlich die Initiative zu ergreifen, wenn es kein anderer tut. Oder, wie würde man es auch nennen? "Aus der Komfortzone herauskommen". Es besteht ein gewisser Mangel an Bewusstsein daran, dass man Zugeständnisse für außergewöhnliche Leistungen nicht auf dem Silbertablett serviert bekommt. Man muss für sich selbst aufstehen oder es wird nichts. Sich in den Vordergrund drängeln (das gilt genauso auch für die Männer).
Darunter bleiben allerdings immer noch einige Denkunterschiede in der Tiefe vorhanden (siehe, dass Östrogene an sich emotionaler machen als Testosteron; nur im Übermaß bewirken das irgendwann beide), es ist nicht so, dass man aus beidem nach Belieben genau das Gleiche formen könnte. Aber das sieht mehr nach Gefühls- und Vorgehensmuster aus, nach Mustern in der geistigen Informationsverarbeitung in Kombination mit ersterem, als nach Fähigkeiten der wirklichen kognitiven Auffassungsgabe.
Zudem... Es ändert nichts an dem Umstand, dass sich eine Person eines bestimmten Geschlechtes tendenziell erst einmal am Habitus des eigenen Geschlechts orientiert, wenn es um Verhaltensweisen (und ganz besonders deren Erlernung) geht. Das macht jeder aus seiner eigenen unterbewussten (natürlichen?) Bestrebung heraus, die einem keiner eingeredet hat.
Die Tendenz des Videos ist nach meinem Verständnis tatsächlich alle Unterschiede als viel kleiner darzustellen als sie im Bewußtsein der Allgemeinheit vorhanden sind. Es ging mir auch nicht darum dies in Frage zu stellen - davon bin ich selbst überzeugt. Es war vielmehr der Gedanke, nein, die pointierte Aussage, die ich zitiert habe, die mir logisch unverständlich, in sich widersprüchlich vorkam.
Selbst wenn diese Aussage nicht zutrifft bleibt der Sachverhalt unbenommen: Es gibt (fast) keine Unterschiede zwischen den Geschlechtern, die anatomisch nachzuweisen wären. Daher sind frühere Aussagen (wie etwa: Frauen haben ein kleineres Gehirn") kompletter Unfug. Die Unterschiede liegen zuerst in der genetischen Tatsache von zweimal "X" anstatt "X" und dem schwächeren "Y" - und in den Hormonen.
Gerade in den Zeiten bis zum Mittelalter, insbesondere in der vor-christlichen Zeit, waren die Aufgaben nicht aus ideologischen Gründen anders verteilt, sondern aus physiologischen Gesichtspunkten wie Kinderkriegen und Kinder betreuen. Das wegzudiskutieren scheint in den letzten Jahren ein wesentliches Anliegen interessierter Kreise zu sein: Wenn die Löhne und Gehälter stagnieren - wie seit Jahrzehnten - dann müssen die Frauen ran und mitverdienen damit das Geld reicht und davon abgelenkt wird was dafür der Grund ist. Das geht am Besten, wenn man die Überzeugungen verschiebt und die Betroffenen selbst erklären lässt, dass es eben "alternativlos" ist und nicht anders geht.
Das Geschlechtermißverhältnis in bestimmten Bereichen und die Frage welche Art von Verhalten man im geschäftlichen Umgang einnehmen sollte halte ich für Nebenkriegsschauplätze die von den Tatsachen ablenken sollen - solange es reine Mänerbetriebe gab war das sonderbarerweise nie eine Frage! Schon immer war es auch so, dass man sich selbst loben und Ansprüche auf höhere Verwendung selbst vorbringen musste - weil es wer anders nicht getan hat.
Der Bereich ist ein bisschen sensibel, weil sich Menschen schnell persönlich auf den Schlips getreten fühlen. Ich muss auch sagen, gerade da Übersee sehr dominierend in kulturellen Dingen ist, ist hier auch eine Menge bizarrer Unsinn hineingeflossen. Unsinn, der darauf hinaus läuft, irgendwie sein eigenes Selbst zu rechtfertigen vor der Gesellschaft - obwohl man das auch wesentlich sachlicher, wesentlich nüchterner angehen könnte mit dem selben Resultat. Persönlich gefällt mir die Art gar nicht.
Ja, das ist es, was ich meine. Ich finde, da sind beim näheren Hinschauen gar nicht mal so viele ideologische Hintergründe dabei, als einfach die Anerkennung physischer Beschaffenheiten.
Als die Religion aus dem Nahen Osten nach Europa kam - da will ich nicht unbedingt streiten, die haben durchaus auf der großen Agenda eine gewisse Form der Zwangseinteilung betrieben. Obwohl die wahrscheinlich auch nicht immer in allen Lebensbereichen so zum Tragen kommen konnte (z. B. was ist mit kleingewachsenen Männern, Männern, die durch Krankheit oder körperliche Schäden nicht erwerbsfähig waren, was ist mit Männern, die ohne ihre Frau als Ordnungshalter aufgeschmissen sind, was ist, wenn der Mann allein nicht genug Geld nach Hause bringt, Witwen usw.).
Diese hat aber lange Zeit dafür gesorgt, dass z. B. Bildung von Frauen außerhalb der wohlhabenden oder adligen Kreisen ferngehalten wurden. Ist heute im Rest der Welt teilweise sogar immer noch der Fall.
Die neuere Art der Geschichtsumdeutung würde ich mit vielerlei Aspekten sehen.
Einerseits - intellektuelle Vermüllung. Wenn den ganzen Tag nur über "Diskriminierung" und "Privilegien" geredet wird, die mit Menschenrasse, Geschlecht und sexueller Orientierung zusammenhängen, redet man nicht über andere Ungerechtigkeiten, die alle betreffen können. Das dürfte auch von etwas höherer Stelle befeuert werden.
Andererseits - Unkenntnis und Unverständnis von Geschichte. Könnte man auch als Folge der wachsenden Bildungsmisere in den westlichen Ländern sehen... Bei der Entstehung des amerikansichen Feminismus hat das auch schon eine Rolle gespielt. - Man liest irgendwelche Schriften, deutet sie im Präsenz statt sie eingebettet in ihren zeitgeschichtlichen und örtlichen Kontext zu setzen, und bastelt sich daraus irgendeine Fantasie-Ideologie, so wie es einem Spaß macht...
Eine dritte Komponente, die man noch sehen könnte: Der strukturelle Verlust dessen, dass die Generationen miteinander kommunizieren und Wissen weitergeben. Von wem soll man schließlich wissen wie manches zu deuten ist, wenn man als Informationsquellen nur die verdrehte politische Agitation der Gegenwart hat? (Das ist sogar eine Sache, die auf beiden Seiten wirkt - bei Jung und bei Alt.)
Ach ja, und - als vierter Faktor: Die Diskussion, entnehme ich vage, rangiert häufig nur auf dem Ansichtspunkt irgendwelcher Mittelstandskinder, die in ihrer wohlbehüteten Welt außer Diskriminierung nichts behinderndes in ihrem Aktionsradius kennen. (Und dann noch, überaus lachhaft: Sie selbst leiden nicht einmal sonderlich an dieser "Diskriminierung", weil ihre soziale Schicht ihnen trotzdessen die Türen öffnet.) Es werden in der Regel nicht die Leute gefragt, die am nächsten an dieser Diskriminierung dran sind oder wo diese sich z. B. in Form von Gewalt manifestiert.
Ich meinte das letzte gar nicht mal in Bezug auf die kapitalistische Geschäftswelt, sondern generell auf "Errungenschaften" bezogen. Errungenschaften idealistischer Natur.
So lang die Bedingungen dafür nicht stimmen, dass es möglich ist, das zu schaffen - okay.
Allerdings haben sich von dem Zustand in der Historie die Bedingungen bereits merklich verändert. Und was passiert? Frauen machen zwar die besseren Bildungsabschlüsse, warten aber scheinbar darauf, dass Scotty sie hochbeamt.
Und beschweren sich, dass das einfach nicht passiert.
Anstatt zu realisieren, so lief das Spiel noch nie.
1. Alleine die Jahrhunderte lange Männerdominanz - die noch anhält und bei der keine Anzeichen für Lockerung zu erkennen sind - spricht gegen eine Anerkennung der Frau als gleichberechtigt und -fähig.
2. Sicher hat die Diskussion Ablenkungspotential - so wie stets, wenn wieder 'eine Sau durchs Dorf getrieben wird' frage ich mich in solchen Fällen immer was hinter dieser Nebelwand passiert das wir nicht sehen sollen.
3. Da bin ich nicht so sicher - schließlich ist es möglich sich zu orientieren, Quellen gibt es zuhauf und wer es will findet immer mehrere Sichtweisen um zu vergleichen und zu sehen was davon plausibler ist und wo die Informationen noch erweitert weden müssen um Klarheit zu bekommen.
4. Diskriminierung gibt es in mannigfaltiger Form, da will ich nicht mal eine Klasseneinteilung machen: Was für ein Kind aus 'besseren Kreisen' schwer zu tragen ist mag vor einem anderen soziologischen Hintergrund läppisch erscheinen, dennoch ist es im Erleben der Betroffenen schwerwiegend. Hier müsste das Augenmerk auf einer breiteren Diskussion liegen was wann als 'tolerabel' anzusehen ist und was nicht. Da hilft aber nur den Einzelfall zu sehen, pauschalisieren lässt sich das mE nicht.
Frauen haben immer das zweischneidige Problem einerseits 'Frauchen' sein zu müssen, andereseits 'ihren Mann stehen' zu sollen - und zwar je nach Situation. Da kapitulieren viele Frauen und lassen doch wieder andere darüber entscheiden .... ich habe Fälle vor Augen in denen aus fähigen, emanzipierten weiblichen Wesen Schnütchen ziehende Weibchen wurden weil sie DEN MANN haben wollten und der darauf abging wenn sie unterwürfig waren. Das ist ein eigenes Kapitel, vor dem selbst ich ein wenig Bammel habe!
Ich würde das als eine Frage der Betrachtung sehen: Man muss sich im Klaren werden, wenn man eine bestimmte Stellung in der Gesellschaft oder der Hierarchie einnehmen will, dann muss man dafür etwas tun. Umsonst gibt es nichts.
Gerade auch, weil eine gewisse Form der Männerhierarchie erst einmal so bleiben wird (gerade die westlich-konservative der BRD und Amerika hat nach wie vor auch noch ihre Probleme damit, eine Frau als intellektuell fähig zu betrachten), wird da ein gewisser Biss gefragt sein.
Und nicht “ach, ich fröhne doch lieber tagtäglich meinen Gefühlsduseleien und spiele Mimose, wenn man mir nicht das gibt, was ich will, ist viel einfacher als sich ins Zeug zu legen und die AGBs des Spiels zu akzeptieren, in dem ich Königin werden will”.
Ein paar haben das im Verlaufe der Geschichte hin und wieder kapiert, und dem entsprechend sind ihre Namen nicht in der Geschichte verblasst.
Das mit dem “Frauchen sein müssen” ist auch so eine Sache. Zunächst frage ich mich dabei: Wer sagt das überhaupt? Ich? Die Gesellschaft? Die Männer? Der liebe Herrgott? Wer sagt das? Wer legt das fest, dass man so sein muss?
Mir schwebt die Position vor “Scheiß doch drauf”. Weil, warum soll das wichtig sein?
Am meisten lügt man sich doch dabei selbst in die Tasche. Man suggeriert sich selbst etwas.
Und wenn manche Typen damit ein Problem haben, da dann, sollen sie doch… Irgendeine dumme Ollsche, die sich verbiegen lässt, finden die garantiert als Ehefrau. There’s plenty of fish in the sea.
‘N Typ, für den man sich verstellen muss, der ist es doch nicht wert. Inklusive allem anderen, was daraus erwachsen kann.
Nächste Frage wäre die: Wer legt denn fest, was “fraulich sein” bedeuten soll?
Also, ob man sich diesen von Menschen gemachten Gepflogenheiten beugt oder nicht, das ist doch wohl ‘ne Sache, die man sich heute selbst aussuchen kann.
Und wenn da ein solcher Trieb wie “biologische Uhr tickt” aus dem Gebüsch feuert, dann muss man dem auch mal in den Arsch treten. Keine Art der Vermehrung ist es wert, dass man dafür sich selbst verbiegt und jeden Idioten als Kindervater nimmt, der nicht bei drei auf den Bäumen ist (und was man im Anschluss daran sein ganzes Leben lang bereut).
Ich sehe bei dem Thema eine Menge Selbstsuggestion – sich selbst etwas einreden bzw. es sich von anderen einreden lassen.
Ich denke, man versteht aber, was ich meine, oder nicht? Leute, die aus wohlbehüteten Verhältnissen stammen, die sich über Formen von Diskriminierung aufregen, die sie selbst in dem Ausmaß nie erfahren haben. Wo ihre gesellschaftliche Stellung, von materieller Seite aus, Diskriminierungen anderer Art in der Praxis neutralisiert haben.
Leute, die sich in ihrer sicheren Blase schier angefangen haben, zu langweilen, und meinen, nun die Welt retten zu müssen.
Ihre Annahme, es sei schwieriger etwas zu erreichen als sich lediglich treiben zu lassen ist zutreffend - und die Folgerung daraus ebenso. Die menschliche Trägheit alerdings ist ersterer Version im Wege, weswegen es wohl nur Wenige schaffen, sich aus der Masse heraus zu heben. Ob das immer die *Richtigen* sind sei dahingestellt.
Was meinen Weibchenhinweis angeht schlagen Sie bitte nicht den Boten! Ich habe lediglich etwas beschrieben, was beobachtet werden kann - keine Bewertung darin. Allerdings muss selbst ich zur Kenntnis nehmen:
Es gibt eine Tendenz diesem Typ eine Renaissance zu verschaffen - schon deswegen, weil sich viele Männer vor gestandenen, emnzipierten Frauen fürchten. Wie vor ihrer Mutter.
Das Thema *Kindsvater* und dessen Rolle hatte ich schon mal früher besprochen - und sollte vielleicht gleich dazu setzen, dass ich diese Frauen für extrem gefährlich halte, die nur einen Samenspender wollen und dabei einerseits die Psyche des Kindes quälen, andererseits verantwortungsvolle Väter in schwere Krisen stürzen.
Da sind wir allerdings nun wirklich sehr weit vom Ausgangsthema abgekommen. Wie das oft so geht ;c)
Ähm, den Boten schlagen hatte ich dabei nicht im Sinn.
Halte man es so fest: Auch ich mache nur meine Beobachtungen. Daher ist mir dieses Verhaltensmuster bekannt.
Obwohl ich dazu sagen muss: Ich verstehe es nicht.
Liegt vielleicht aber eher daran, dass für mich schon frühzeitig die Fragen aufkamen, wer schreibt mir vor, was ich befolgen muss? Warum soll ich dieses oder jenes tun, nur um mich in meiner Rolle als was auch immer zu beweisen?
(Man kann das in beide Richtungen verstehen, für Frauen als auch Männer.)
Und heraus kam für mich die Einstellung "fickt euch, Leute, ich mache mein eigenes Ding, ich folge meinen Instinkten".
Kann sein, dass ich das dewegen nicht verstehe.
Wenn ich das mal so sagen darf... Von außen betrachtet, verstehe ich an der Stelle ebenso nicht, warum sich Frauen dort solche Sorgen machen. Machen sie sich Sorgen darum, allein zu enden? Als vertrocknete Jungfer zu sterben?
Was soll dieser Unsinn. An der Stelle kommt es mir vor, als wenn Frauen sehr anfällig für die kleinsten Manipulationen sind. Ein bisschen weniger in Emotionen schwelgen könnte ihnen manchmal gut tun. Damit man das Wichtige vom Unwichtigen unterscheiden lernt.
Nun, selbst wenn man Verhalten beobachtet muss das noch lange nicht bedeuten, dass man es auch deuten kann, nicht einmal, dass es absolut gedeutet werden könnte. Manches mag von aussen betrachtet schlüssig und erklärbar erscheinen - und doch hat es eine völlig verschiedene Ursache oder Bedeutung von dem was sich als Eindruck aufdrängt.
Sich in die Gedanken- und Gefühlswelt eines / des anderen Geschlechts hineinzudenken ist wohl schlichtweg unmöglich, da mit der genetischen Determination (die viele Varianten haben kann, mindestens aber zwei, wie beim Menschen) auch die Gefühlswelt bestimmt wird. Dazu kommt noch die innerartliche Variabilität - und schon wird es schwierig, ja, wie ich meine unmöglich, das zu erfassen.
Welche Sorgen Frauen haben kann ich daher nur vermuten und aus dem folgern, was ich in Gesprächen gehört habe. Allerdings wage ich selbst mit fast 75 da keine endgültige Aussage.
Ach, noch ein Hinweis:
Mit der Aussage ihres letzten Absatzes sollten Sie Frauen gegenüber vorsichtig sein, das könnte Ihnen Schwierigkeiten im Umgang machen ;c)
Ja und nein.
Sicherlich, ich werde manches nicht nachvollziehen können, weil ich - als Ego - nicht in der Situation stehe und dazu eine völlig andere Einstellung habe.
Auf der anderen Seite ist es mir aber auch bewusst, wie sehr so etwas formbar ist.
Theoretisch könnte ich auch ein Schlappschwanz sein, der sich in dieser Hinsicht alles überstülpen lässt - mache ich aber nicht, weil es eine gewisse Grenze für mich gibt, ab wo ich mir fremdbestimmte Dinge nicht mehr bieten lasse. Wo ich die Kontrolle darüber behalten will. Wo mein Wille sagt "in diese Richtung will ich nicht" und auch bereit dazu ist, das konsequent durchzuziehen.
Und das ist eine mentale Angelegenheit; das hat etwas mit mentalen Fähigkeiten, Willen und Willensstärke zu tun.
An der Stelle frage ich mich natürlich: Was hält Frauen nun davon ab, auf einen ähnlichen Status zu kommen?
Und ich meine das eben auch als Frage, wo es genauso genügend männliche Protagonisten gibt, die sich durch das Leben treiben lassen bis sie 40 sind und dann fangen sie auf einmal an, als Persönlichkeit Grenzen zu ziehen, in welche Richtung sie gehen und nicht gehen wollen.
Mir kommt das an der Stelle vor, als wenn man Persönlichkeiten so herangezogen hat, dass sie ihr Leben lang mit Orientierungs- und Selbstwertproblemen zu tun haben. Nach dem Motto "ich bin es nicht wert, darum muss ich schnellsmöglich sehen, wo ich bleibe". Nur sagt es den Protagonistinnen keiner, ihr Leben lang, bzw. wenn es ihnen gesagt wird, lieber wird ausgerastet oder in der Ecke endlos herumgeheult und die Wahrheit abgewehrt anstatt etwas damit anzufangen. Wie als wenn man ein kleines hilfloses Kind ist und kein Erwachsener. "Mama, bitte komm zurück, ich will die Symbiose wiederhaben"... Sowas in der Art.
Über solcherlei habe ich aufgehört, mir zu viele Gedanken zu machen. Ich bin schon fast von Beruf "die Stimme des Verderbens" und im Zwischenmenschlichen "der Arsch vom Dienst" (auch wenn ich ein gewisses Gespür habe, was angebracht ist und was nicht)
Ist natürlich auch eine Frage, ob man überhaupt Damen bezirzen will oder nicht, hehe.
@ matrixmann
".. 1. Wo ich die Kontrolle darüber behalten will.
2. Wo mein Wille sagt "in diese Richtung will ich nicht" und auch bereit dazu ist, das konsequent durchzuziehen.
3. Und das ist eine mentale Angelegenheit; das hat etwas mit mentalen Fähigkeiten, Willen und Willensstärke zu tun .."
zu 1.
Es gibt Situationen in denen man sich einer anderen Person hingeben muss, da wäre es für die Beziehung schlecht wenn man 'Kontrolle behalten' will.
zu 2.
Prinzipien zu haben ist eine gute Sache - allerdings nicht ohne jedes Mal darüber nachzudenken ob es in dieser speziellen Situation angemessen ist das durchzusetzen. Es kann besser sein nachzugeben um dann später ein besseres Ergebnis zu erzielen.
zu 3.
Volle Zustimmung! Wenn man eine Entscheidung getroffen hat soll man dabei bleiben und nur abweichen, wenn völlig neue Perspektiven eröffnet werden.
Es wird wohl eher ein rhetorische Frage sein was 'Frauen' (also deren Gesamtheit?) davon abhält manchmal konsequent zu sein? Ich führe das auf eine andere Art zu denken zurück, die stets Harmonie und Gemeinsamkeit vor Durchsetzung einer bestimmten Sache zum Ziel hat. Frauen verlieren das Ziel dabei nicht aus den Augen, sie warten auf einen 'schwachen' Moment um es zu erreichen.
Wenn Erziehung überwiegend von Frauen geleistet wird und wenig männlicher Einfluss vorhanden ist mag das was sie da postulieren richtig sein. Deswegen ist es ja so bedeutsam den Vätern auch bei gescheiterten Beziehungen Kontakt zu ihren Kindern zu ermöglichen.
Wir bewegen uns hier auf lockerem Sand, denn erstens führt es von der Ausgangsfrage weg - und zweitens fehlen da die Daten um eine These zu formulieren und ihre Relevanz zu prüfen. Es ist ein Meinungsaustausch, der schon von einer dritten Person völlig anders bewertet werden kann.
Wenn ich einen 'bezirzen'-Rat anfügen darf ("Fragen Sie den Briefkastenonkel"):
Das Ziel im Auge haben und nicht direkt darauf zusteuern, sondern genau beobachten welche Träume, Wünsche, Vorstellungen vorhanden sind und diese in eigenes Tun einzubeziehen - das bedeutet sich damit auseinanderzusetzen und die eigene Sicht anzudeuten, mit der Bereitschaft graduell Zugeständnisse zu machen - ist hier der Weg zum 'Erfolg'.
Völlig unabhängig davon, WAS das verfolgte Ziel ist. Man zeigt Interesse und Einfühlungsvermögen. Mehr geht nicht.
*edit*
Oder doch, siehe dazu diesen Kommentar, die zugehörige Diskussion, und den Artikel.
Hingabe bedeutet nicht "Selbstaufgabe" - jedenfalls sollte sie das nicht.
Menscheln beinhaltet das Problem, wenn man zu viel davon praktiziert und anderen nicht auf die Füße treten will, dann hält man zu oft das Maul, wo es angebracht wäre, es aufzumachen.
Wie ging der Spruch? "Das muss die Demokratie aushalten"? Menschen müssen hin und wieder auch mal was aushalten. Das Leben ist weder ein Ponyhof, noch bringt einen vieles aus der Rubrik "bloß nicht aus der Komfortzone herausholen" weiter.
Keine Ahnung, ob es eine rhetorische Frage ist.
Jedenfalls muss ich sagen, mit der Methode, es allen Recht machen zu wollen, damit wird man nur der Sklave und der Spielball der Wünsche anderer. Wenn man selbst etwas bestimmtes will, und es einem wirklich wichtig ist, dann muss man das selbst vorantreiben. Die Methode "sieht man das nicht?!" funktioniert nicht, denn a) kann keiner Gedanken lesen und b) es ist immer abhängig davon, ob es das Gegenüber überhaupt tangiert. Jemandem, dem du scheißegal bist, der wird nicht auf deine Wünsche eingehen (und davon gibt es mehr Menschen auf der Welt als solche, denen man nicht egal bist, weil sie dich alle nicht einmal kennen).
Ist wirklich eine Frage, ob man versteht wie die Welt grundlegend funktioniert oder ob man lieber in seiner kleinen Blase verweilen will, wo man selbst die Hauptrolle spielt und alle nicht anders können als sich nach einem zu richten. (Ob man dem Prinzessinnen-Syndrom weiter fröhnen will oder die Wahrheit akzeptiert, dass man keine ist.)
Kritisch ist das mit dem überproportionalen Anteil von Frauen in den Erziehungsberufen, mit denen man beim Aufwachsen konfrontiert wird, eher in der Hinsicht, weil man potentiell kein grundlegend anderes Modell Persönlichkeit vorgelebt bekommt. Frauen können zwar selbst sehr unterschiedliche Charaktere haben (da können auch ziemliche Drachen und Giftspritzen darunter sein...), aber erwachsene Männer sind noch einmal etwas anderes, weil sie doch teilweise sehr anders sozialisiert werden, physisch ist es auch ein Unterschied, da sie aus einer größeren körperlichen Leistungsfähigkeit heraus ganz andere Bestrebungen und Handlungsweisen haben können.
Wirklich schlimm ist dieser Faktor speziell, wenn Jungen ohne Vater oder ähnliche Figuren aufwachsen, weil ihnen dann die Erfahrung fehlt, dass jemand körperlich stärker als sie sein kann und sie nicht der König der Welt sind. Sobald sie groß genug sind, kann es sein, dass die Mütter ihnen physisch nicht mehr Herr werden, weil sie bereits schon so viel mehr Kraft als diese haben. (In diesem Punkt sind auch sehr alte Väter ein kritischer Aspekt.)
Das ist mehr ein wesentlicher Punkt, warum das gar nicht so gut ist. - Zudem, dass auch die Väter (genauso wie die Mütter) eine Vorlage für die späteren partnerschaftlcihen Beziehungen abgeben.
Keine Erfahrung bedeutet an der Stelle nämlich "keine Erfahrung". Kein Muster, wie man mit Männern umgeht, was man von ihnen erwarten könnte, wie sie evtl. funktionieren, sowie keine Form von gesunder Vorsicht (z. B. welchen man lieber grundsätzlich aus dem Weg geht) und kein gesundes Bild, wann man sich jemandem gegenüber abgrenzen sollte (z. B. wenn sich ein Mann erst später zum Tyrann entwickelt, oder wenn er zeitweise übel ist, aber sich dann mit großen Versprechungen entschuldigt, nur um sich dann wieder scheiße zu verhalten).
Der letzte Satz war zwar anders gemeint, aber ich belasse es dabei einmal. Würde mir zu persönlich werden...
> Hingabe bedeutet nicht "Selbstaufgabe" - jedenfalls sollte sie das nicht.
Stimmt, allerdings bedeutet es sich aus dem Schneckenhaus heraus zu begeben. Geht bei den Schnecken auch, sie behalten ihr Haus ....
> Menscheln beinhaltet das Problem, wenn man zu viel davon praktiziert und anderen nicht auf die Füße treten will, dann hält man zu oft das Maul, wo es angebracht wäre, es aufzumachen.
Ich bin bestimmt der letzte, der dem JA-Sagen das Wort reden würde - und trotzdem muss man sehr genau überlegen ob es nicht besser ist in manchen Situationen zu schweigen und dann später umso effektiver den anderen Standpunkt zu vertreten.
"Angriff ist NICHT immer die beste Verteidigung!"
> Wie ging der Spruch? "Das muss die Demokratie aushalten"? Menschen müssen hin und wieder auch mal was aushalten. Das Leben ist weder ein Ponyhof, noch bringt einen vieles aus der Rubrik "bloß nicht aus der Komfortzone herausholen" weiter.
Auch das ist sicher prinzipiell richtig, wenn es angemessen dosiert wird: Nicht jede/r hat eine eiserne Konstitution, Aufwand in Inkrementen ist letztlich auch eine Form der Zielerreichung.
> Keine Ahnung, ob es eine rhetorische Frage ist.
> Jedenfalls muss ich sagen, mit der Methode, es allen Recht machen zu wollen, damit wird man nur der Sklave und der Spielball der Wünsche anderer. Wenn man selbst etwas bestimmtes will, und es einem wirklich wichtig ist, dann muss man das selbst vorantreiben. Die Methode "sieht man das nicht?!" funktioniert nicht, denn
a) kann keiner Gedanken lesen und
b) es ist immer abhängig davon, ob es das Gegenüber überhaupt tangiert. Jemandem, dem du scheißegal bist, der wird nicht auf deine Wünsche eingehen (und davon gibt es mehr Menschen auf der Welt als solche, denen man nicht egal bist, weil sie dich alle nicht einmal kennen).
Es allen recht machen zu wollen ist nie eine gute Idee - mindestens nicht, wenn diese Gruppen/Menschen aufeinander treffen könnten und der Schmu herauskommt Einen Standpunkt zu haben und zu verteidigen ist richtig - nur darf man nicht vergessen, ab und zu zu prüfen, ob das noch angemessen ist oder ob es Gründe gibt hier nachzujustieren. Wenn man etwas erreichen will muss man es selbst betreiben, richtig, weil es niemand anderer für einen tut.
> Ist wirklich eine Frage, ob man versteht wie die Welt grundlegend funktioniert oder ob man lieber in seiner kleinen Blase verweilen will, wo man selbst die Hauptrolle spielt und alle nicht anders können als sich nach einem zu richten. (Ob man dem Prinzessinnen-Syndrom weiter fröhnen will oder die Wahrheit akzeptiert, dass man keine ist.)
siehe b) weiter oben.
> Kritisch ist das mit dem überproportionalen Anteil von Frauen in den Erziehungsberufen, mit denen man beim Aufwachsen konfrontiert wird, eher in der Hinsicht, weil man potentiell kein grundlegend anderes Modell Persönlichkeit vorgelebt bekommt. Frauen können zwar selbst sehr unterschiedliche Charaktere haben (da können auch ziemliche Drachen und Giftspritzen darunter sein...), aber erwachsene Männer sind noch einmal etwas anderes, weil sie doch teilweise sehr anders sozialisiert werden, physisch ist es auch ein Unterschied, da sie aus einer größeren körperlichen Leistungsfähigkeit heraus ganz andere Bestrebungen und Handlungsweisen haben können.
Na, wer breitet da das Gender-Vorurteil aus? Es gibt mindestens so viele toughe Frauen wie Männer und umgekehrt gilt das genau so für Softies.
Das Frauen in den Erziehungsberufen dominieren ließe sich schnell ändern, wenn man die Bezahlung anders regeln würde bzw. jetzt (immer noch) verschlossene Bereiche für Frauen öffnen würde, damit sie dahin abwandern können.
> Wirklich schlimm ist dieser Faktor speziell, wenn Jungen ohne Vater oder ähnliche Figuren aufwachsen, weil ihnen dann die Erfahrung fehlt, dass jemand körperlich stärker als sie sein kann und sie nicht der König der Welt sind. Sobald sie groß genug sind, kann es sein, dass die Mütter ihnen physisch nicht mehr Herr werden, weil sie bereits schon so viel mehr Kraft als diese haben. (In diesem Punkt sind auch sehr alte Väter ein kritischer Aspekt.)
Zustimmung, allerdings sollte *körperliche Stärke* nicht in der Erziehung dominieren. Es geht um Geduld, Argumente und Konsequenz - und da stimme ich zu, dass Frauen oft Harmonie im Sinn haben und dabei diese drei Grundsätze vergessen.
> Das ist mehr ein wesentlicher Punkt, warum das gar nicht so gut ist. - Zudem, dass auch die Väter (genauso wie die Mütter) eine Vorlage für die späteren partnerschaftlichen Beziehungen abgeben.
> Keine Erfahrung bedeutet an der Stelle nämlich "keine Erfahrung". Kein Muster, wie man mit Männern umgeht, was man von ihnen erwarten könnte, wie sie evtl. funktionieren, sowie keine Form von gesunder Vorsicht (z. B. welchen man lieber grundsätzlich aus dem Weg geht) und kein gesundes Bild, wann man sich jemandem gegenüber abgrenzen sollte (z. B. wenn sich ein Mann erst später zum Tyrann entwickelt, oder wenn er zeitweise übel ist, aber sich dann mit großen Versprechungen entschuldigt, nur um sich dann wieder scheiße zu verhalten).
Wie wir lernen was gut und richtig und was falsch und zu unterlassen ist wird tatsächlich eher durch Vorbild als durch eindringliche Sätze von Elternseite erreicht. Das wird häufig unterschätzt: Kinder beobachten und denken sich ihren Teil, und wenn Beobachtung und Belehrung auseinander driften ist das der Tod jeder Erziehungsarbeit. Genauso wie zu viel *erhobener Zeigefinger* und ständige Ermahnungen - da geht es bald 'hier-rein-und-da-raus', der Effekt ist umgekehrt proportional zur Menge der Worte
Hat für mich mehr was mit "Selbstwahrung" zu tun. Gut, das ist nicht "Hingabe", ist aber etwas, dass in den Überlegungen oftmals viel zu kurz kommt.
Mir selbst ist das sehr wichtig.
Hm, sehe ich nicht den Angriff drin.
Wie soll ich es ausdrücken? Ich denke, ich bin nicht sehr auf "Harmonie" gestrickt - oder wenn, dann sollte sie wenigstens ehrlich sein und von Herzen kommen. Harmonie, die auf "Maul halten" beruht, ist schließlich nur ein Trugbild, dass früher oder später zusammenbricht. Je länger man das Maul hält, umso heftiger wird es werden.
Nein, das, was ich meine, hat nichts mit Gender-Vorurteilen zu tun.
Gut, es ist wahrscheinlich eher eine Frage von potentiellen Szenarien, von "etwas, was im Durschnitt zu erwarten ist". Nichtsdestotrotz, in den Feinheiten macht es doch einen leichten Unterschied aus. Und der feine Unterschied macht scheinbar doch mehr aus, als man denkt.
Letztendlich, der Fokus sollte hier trotzdem auf "verschiedene Persönlichkeitsmodelle" liegen - da ist "männlich sein" nur eine Schlüsselkomponente, die potentiell für größere Abweichungen sorgen kann.
Eine Sache, um dem überproportionalen Anteil an Frauen in den Erziehungsberufen entgegen zu wirken würde ich darin sehen, einerseits erst mal das Vorurteil/die Unterstellung abzubauen, dass, wer als Mann in solche Berufe geht, nur pädophil sein kann (und darum benötigt es keine Förderung, auch Männer in diesen Berufen zu haben) - zum anderen, auch das klassische Vorurteil (und die dementsprechende Indoktrinierung von Kindesbeinen an) abzubauen, dass Frauen wie "dafür geschaffen sind", mit Kindern umzugehen. Dass Frauen automatisch gut mit Kindern umgehen können. Das war früher schon Käse, und gerade das Beispiel mit dem Spielzeug, was man dem Kind vorsetzt, sollte es eigentlich klar mann, dass der Fokus auf Menschen und sich um sie zu kümmern (kümmern zu können) auch etwas mit "Antrainieren" zu tun hat.
Das mit der körperlichen Stärke hat nur begrenzt etwas mit Autorität zu tun. Es geht um etwas, was allgemein unter "Raum begrenzen" zu verstehen ist. Ein bisschen spielt die physische Komponente darin hinein, weil Raumbegrenzung gleichzeitig immer mit voraussetzt, dies auch durchsetzen zu können.
Auf einen Schwätzer, bei dem es nur bei den Worten bleibt, auf den hört keiner - und gerade Kinder in der Entwicklung sind sensibel dafür, die Widersprüche und Schwächen ihrer Beziehungspersonen wahrzunehmen. Sie sich auch zu Nutze zu machen.
Speziell wenn Kinder älter werden und selbst allmählich Kraft entwickeln, die es mit der eines Erwachsenen aufnehmen kann, braucht es etwas, was sie in dieser Hinsicht erdet, damit im Kopf die Lehre zurückbleibt "ich bin nicht der Größte und der Stärkste". Verstehen sie, die Verdeutlichung des Umstandes "du bist nicht unantastbar".
Ab einem gewissen Punkt geraten Mütter dort ins Hintertreffen, weil Testosteron ganz einfach mehr Muskelkraft gibt. Ältere Väter tun dies auch, aber dies liegt dann daran, dass sie schlichtweg schon mit zu vielen Gebrechen zu tun haben, um einem Pubertierenden, der seine 5 Minuten kriegt, im Ernstfall in die Schranken weisen zu können. (Ein alter Mann könnte es schließlich auch allgemein schwieriger direkt mit einem Säbelzahntiger aufnehmen.)
Ich meinte nicht "Mahnungen" über Richtig und Falsch in dem Punkt, sondern die Vorlage für die spätere Beziehungsfähigkeit eines Menschen.
Mütter spielen hier zwar eine Rolle wie die Tendenz mit Menschen allgemein aussieht, Väter sind aber dafür wichtig - insbesondere bei auf Männer orientierte Menschen -, wenn es darum geht, sie einschätzen zu können.
Keine Erfahrung - weil es keinen Vater oder eine ähnliche Figur gab, oder der Vater sehr wenig im Leben abwesend war - bedeutet in dem Punkt, völlig unbeholfen später an die Sache heranzugehen. Das heißt aber auch: Ohne jegliche Vorsicht. Ohne inneres Bild davon, was darf der andere von einem verlangen und was nicht, weil es absolut grenzüberschreitend ist.
Kurz gesagt: Nie lernt man vor den ersten Beziehungen einen Mann so intensiv kennen wie den eigenen Vater. Und wenn diese Erfahrung fehlt, dann weiß man nicht, auf was man achten muss, wovor man sich hüten muss, wenn man sich ihnen selbst zuwendet. (Wenn der Alte ein Arsch war, dann in die Richtung, dass man Dinge als "normal" ansieht, die es in einer Beziehung eigentlich nicht sein sollten.)
PS: Ich bin in Sachen "psychologisches Wissen" vorbelastet, so sollte man meine Ausführungen verstehen. Für denn Fall, dass man das nicht erkennen sollte.
" .. Es lassen sich keine geschlechtsspezifischen Ausprägungen bestimmter [Gehirn-] Areale erkennen. Tatsächlich sind die Unterschiede der Fähigkeiten innerhalb eines Geschlechts größer als zwischen den Geschlechtern .. "
Die Unhaltbarkeit von Prof. Lesch’s Aussage lässt sich auch durch ein Parallelbeispiel illustrieren:
Tatsächlich sind die Unterschiede der Körpergrößen innerhalb eines Geschlechts größer als zwischen den Geschlechtern (siehe Pygmäen vs. Longinus-Club). Daraus abzuleiten, "es lasse sich kein geschlechtsspezifischer Unterschied in der Körpergröße erkennen", ist ein offenkundiger Fehlschluss nach dem gleichen Schema wie jener über die geschlechtsspezifischen Ausprägungen der [Gehirn-] Areale. Auch Prof. Lesch wird kaum bestreiten wollen, dass Männer im allgemeinen eben größer als Frauen derselben Ethnie sind.
@ nömix
Prima, Herr nömix, das ist eine gute Möglichkeit es viel anschaulicher zu machen als ich es tat. Zugleich ist es wieder einmal so ein Fall in dem ich mir sage "Warum ist mir das nicht so eingefallen?"
Herzlichen Dank für diese Erklärungsvariante!